T.P.4 Radioactivité
Dans ce TP, on aborde les phénomènes aléatoires comme les jets de dés ou les désintagrations radioactives des noyaux instables.
On se propose de trouver les lois mathématiques permettant de rendre compte de l'évolution d'une population de noyaux radioacifs.
1) Ecart-type et variance
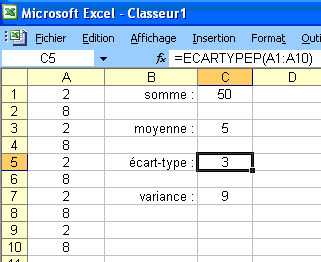
Sans formule mathématique, on voit à partir des exemples suivants, que l'écart-type est l'écart moyen par rapport à la moyenne, et que la variance est le carré de l'écart-type.
. . . . . .
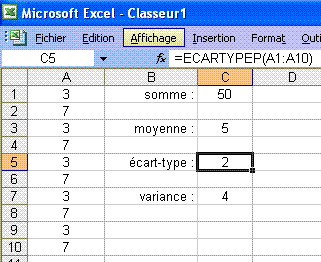2) Caractère aléatoire des jets de dés
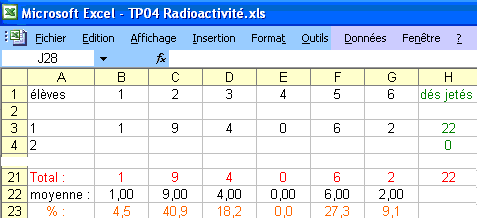
Lors du premier jet de l'ensemble des 22 dés, les pourcentages d'apparition des différentes faces des dés peuvent aller de 0 à 41 % comme ci-dessous :
. . . . . .
Mais après un grand nombre de jets, l'expérience montre que les pourcentages d'apparition des différentes faces des dés tendent vers 16,7 %.
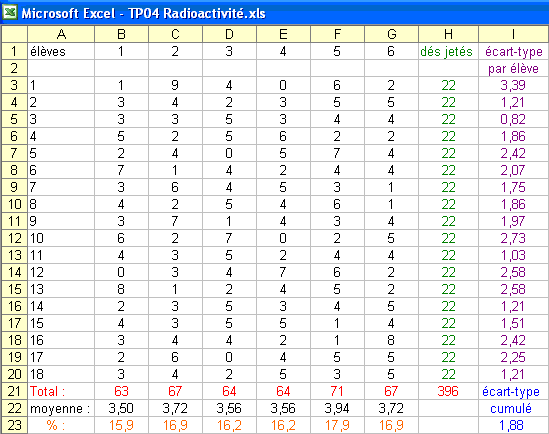
3) Caractère aléatoire des désintégrations radioactives
On étudie les désintégrations radioactives suivantes :
13755 CS —> 13756 Ba + 0-1 e. . . . . . réaction β-
ou :
13755 CS —> 13756 Ba* + 0-1 e. . . . . . réaction β-
suivie de :
13756 Ba* —> 13756 Ba + 00 γ. . . . . . réaction γ
Avec le logiciel Généris, on procède successivement à 30, 300, 1000 puis 3000 comptages du nombre de désintégrations détectées par le compteur situé à 4,5 cm de la source radioactive, avec 3 écran de plomb.
. . . . . .
| comptages |
30 |
300 |
1000 |
3000 |
| résultat |
|
|
|
|
| moyenne |
6,00 |
6,22 |
6,30 |
6,29 |
| écart-type |
2,78 |
2,64 |
2,52 |
2,50 |
| variance |
7,73 |
6,97 |
6,35 |
6,27 |
L'expérience montre que plus le nombre de comptages augmente, plus la répartition des résultats est régulière autour de la valeur moyenne.
Si les désintégrations radioactives sont alléatoires ou imprévisibles, elles ont lieu selon une loi statistique qui est d'autant mieux vérifiée que le nombre de comptage est grand.
4) Simulation de décroissance radioactive
On considère un troupeau de 6000 moutons pouvant être soumis à une "mort aléatoire sans vieillissement".
Avec un tableur on obtient une courbe donnant le nombre de moutons (vivants) en fonction du temps :
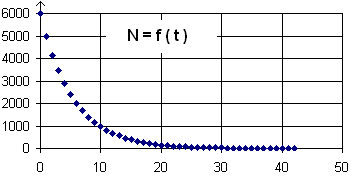
la courbe de tendance est : N = 6000 . e - t/6
De même, on obtient la courbe donnant la variation du nombre de moutons en fonction du temps :
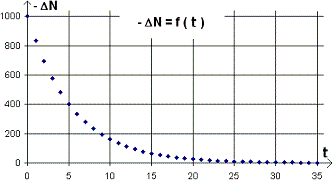
On remarque que la variation du nombre de moutons est proportionnelle au nombre de moutons :
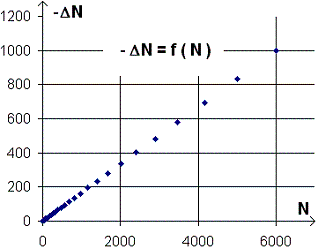
