
T.P.3 Diffraction
1) Diffraction des ondes à la surface de l'eau
| Caractéristiques : |
Dispositif : |
Fronts d'onde |
Ondes rectilignes |
|
|
obstacle rectiligne |
|
|
fente large |
|
|
fente étroite |
|
|
2) Diffraction de la lumière par une fente
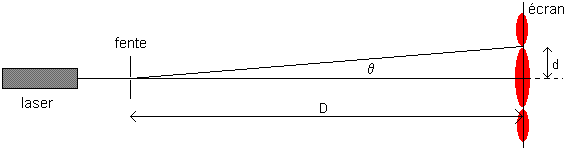
On fait passer un faisceau laser à travers différentes fentes verticales de largeur a comprise entre 40 et 400 `μ`m.
Sur un écran situé à la distance D de la fente diffractante, on observe une figure de diffraction de forme rectiligne (perpendiculaire à la fente diffractante).
ligne
ligne
La figure de diffraction est composée de taches de longueur d, entourant une tache centrale de longueur 2 d.
ligne
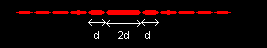
ligne
| fente large |
|
| fente étroite |
|
L'expérience montre que la largeur d de la demi-tache centrale est :
. . . . . - proportionnelle à la distance D entre la fente et l'écran ;
. . . . . - inversement proportionnelle à la largeur a de la fente diffractante.
A partir des mesures de d faites avec les 7 fentes calibrées de largeur a, on trace le graphe : . . d = f(`D/a)`.
Le graphe obtenu est une droite passant par l'origine, dont l'équation peut s'écrire : . . d = k . `D/a`
. . où k est le coefficient directeur de la droite.
Le calcul de la valeur de k donne une grandeur de l'ordre de la longueur d'onde `λ` de la lumière émise par la source laser.
L'expérience permet donc d'établir la relation : . .d = `λ` . `D/a`
3) Diffraction de la lumière par un trou circulaire
On obtient des taches de diffraction de forme circulaire (appelées taches d'Airy) quand la lumière est diffractée par un trou circulaire.












