Exercice 6D
Exercice sans calculatrice
Enoncé :
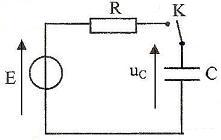
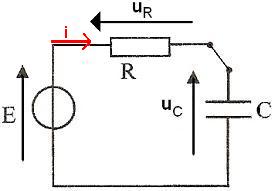
Considérons le montage électrique suivant, comprenant :
. . . - un générateur de tension constante continue E = 12 V ;
. . . - une résistance R = 100 Ω ;
. . . - un interrupteur K ;
. . . - un condensateur de capacité C.
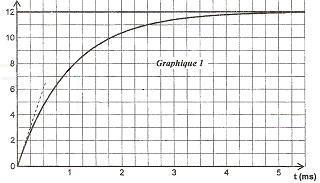
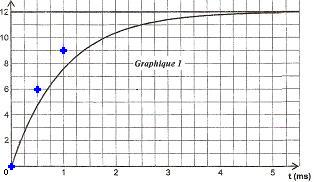
Le condensateur étant déchargé, on ferme l'interrupteur à t = 0. Un système d'acquisition permet d'enregistrer les graphes des tensions E et uc en fonction du temps. On obtient les courbes du graphique suivant.
. . . Aide au calcul : . . . 0,37 . 12 ≈ 4,4 . . . 0,63 . 12 ≈ 7,6 . . . π2 ≈ 10.
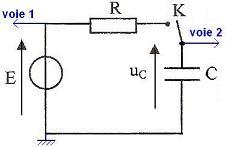
1. Indiquer les branchements du système d'acquisition pour avoir sur la voie 1 la tension E, et sur la voie 2 la tension uc.
2. U et τ étant des constantes, la tension uC est telle que : uC = U [ 1 - exp(-`t/τ`)]
2.a. Déterminer graphiquement U.
2.b. Nommer τ. Déterminer graphiquement la valeur de τ.
2.c. Que représente 5 τ ?
3.a. Etablir l'équation différentielle donnant l'évolution de la tension uC lors de la charge.
3.b. Montrer que uC = U [ 1 - exp(-`t/τ`)] est bien une solution de cette équation différentielle. Exprimer U et τ en fonction des grandeurs caractéristiques du montage.
3.c. Vérifier la dimension de τ par une analyse dimensionnelle.
4. La capacité C du condensateur est : C = 10 µF.
4.a. A l'aide de l'équation différentielle établie à la question 3.a., déterminer la valeur initiale de la dérivée (`(du_C)/(dt)`)0.
4.b. En appliquant la méthode d'Euler, calculer la valeur de la tension uC à la date t = 0,50 ms.
4.c. En appliquant la méthode d'Euler avec un pas Δt = 0,50 ms, compléter le tableau suivant :
t ( ms ) uC ( V ) `(du_C)/(dt)` ( V.s-1 ) 4.d. Porter les points calculés sur le graphique 1. Conclusion ?
Solution :
1. Branchements des voies 1 et 2 et de la masse du système d'acquisition :
2.a. La tension uC est telle que : uC = U [ 1 - exp(-`t/τ`)]
. . . Si t —> ∞ . . . alors exp(-`t/τ`) —> 0. . . et uC —> U
U est égal à la valeur de uC lorsque t —> ∞
D'après le graphique 1, on obtient : U = 12 V.
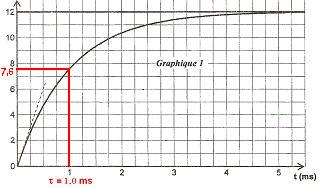
2.b. τ est la constante de temps du dipôle RC.
t = τ lorsque 63 % de la charge du condensateur est réalisée :
. . . D'où : . . . τ = 1,0 ms.
2.c. . . . 5 τ est le temps au bout duquel 99 % de la charge du condensateur est réalisée.
3.a. Choisissons les orientations suivantes :
L'additivité des tensions s'écrit : . . . uC + uR = E. . . ( 1 )
La loi d'Ohm s'écrit : . . . uR = R . i
La relation charge-intenité s'écrit : . . . i = `(dq)/(dt)`
La relation charge-tension s'écrit : . . . q = C .uC
La loi d'Ohm donne : . . . uR = R . `(dq)/(dt)` = R . C . `(du_C)/(dt)`
La relation ( 1 ) donne alors :
uC + R . C . `(du_C)/(dt)` = E. . . ( 2 )
3.b. Si la tension uC est telle que : uC = U [ 1 - exp(-`t/τ`)];
. . . alors, . . . `(du_C)/(dt)` = + `U/(τ)` . exp(-`t/τ`)
. . . D'où : . . . uC + R . C . `(du_C)/(dt)` = U [ 1 - exp(-`t/τ`)] + R . C .`U/(τ)` . exp(-`t/τ`) = U - U exp(-`t/τ`) + U .`(R*C)/(τ)` . exp(-`t/τ`)
Comme cette relation doit être vraie quelque soit t, on obtient 2 égalités :
U = E. . . et . . . τ = R.C
3.c. A partir de la relation ( 2 ), on peut écrire :
. . . [uC] = [R . C] . `([u_C])/([t])`
. . . D'où : . . . [R . C] = [t] = T
4.a. L'équation ( 2 ) donne :
R . C . `(du_C)/(dt)` = E - uC
. . . D'où :
`(du_C)/(dt)` = `(E - u_C)/(RC)`. . . ( 3 )
Or, à t = 0, uC = 0, donc (`(du_C)/(dt)`)0 = `(E - 0)/(RC)` = `E/(RC)`
. . . A.N. : . . . (`(du_C)/(dt)`)0 = `(12)/(1*10^-3)` = 12 . 103 V.s-1.
4.b. Sachant que uC(t + Δt) = uC(t) + `(du_C)/(dt)` . Δt
on obtient : uC(Δt) = uC(0) + `(du_C)/(dt)` . Δt
. . . A.N. : . . . uC(Δt) = 0 + 12 . 103 . 0,50 . 10-3 = 6 V.
4.c. En poursuivant de la même manière, on obtient le tableau :
t ( ms ) uC ( V ) `(du_C)/(dt)` ( V.s-1 )
4.d. Portons les 3 valeurs de uC sur le graphique 1 :
Les 3 points obtenus étant relativement éloignés de la courbe uC(t), on peut remarquer qu'avec le pas choisi, la méthode d'Euler donne une approche assez grossière de cette courbe.
Remarque : Avec un pas plus petit (Δt = 0,25 ms ou Δt = 0,10 ms) les écarts entre les valeurs calculées par la méthode d'Euler et celles mesurées expérimentalement, auraient été plus petits.