
Exercice 2A
Enoncé :
Dans une revue publiée au XIXème siècle, on pouvait lire le texte suivant :
« Les recherches les plus importantes au sujet de la vitesse de propagation du son dans l'eau ont été faites en 1827 sur le lac de Genève.
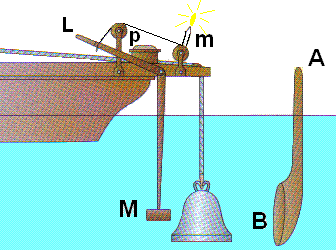
Un marteau peut frapper une cloche suspendue dans l'eau. Le levier L, qui manœuvre le manche du marteau, entraîne une mèche allumée m qui vient mettre le feu à un tas de poudre p à l'instant même du choc. L'éclair résultant de cette inflammation avertit l'observateur, qui doit percevoir le son à distance, du moment précis où la cloche est frappée.
Pour recueillir le son à travers l'eau, cet observateur applique l'oreille à l'orifice A d'un tube en tôle dont la partie plongée dans le lac s'évase en un large récepteur B tourné du côté de la cloche.
Dans ces conditions, le son était perçu en 9 secondes et 4 dixièmes à la distance de 13 487 m. »
a) Quelle durée obtiendrait-on dans l'air pour parcourir les 13 487 m ?
b) Pensez-vous qu'il soit possible d'entendre, à cette distance, le bruit du marteau sur la cloche pour une expérience réalisée dans l'atmosphère ?
. . Quelles informations l'expérience décrite apporte-t-elle pour la propagation du son dans l'eau comparée à la propagation dans l'air ?
c) Quelle valeur de célérité du son dans l'eau cette expérience donne-t-elle ?
d) Décrire le protocole d'une expérience permettant aujourd'hui de mesurer la célérité du son dans l'eau. On fera la liste du matériel indispensable.
Solution :
a) Dans l'air où sa célérité est environ de v = 340 m.s-1, pour parcourir la distance d = 13 487 m, le son mettrait une durée t telle que : t =
. . A.N. . . t = = 39,7 s.
b) On peut imaginer que par temps calme le son de la cloche soit audible à 1 ou 2 km, mais sans doute pas à 13 km! En effet, l'amplitude du son de la cloche sera trop faible à cette distance pour différentes raisons.
. . D'une part à cause de l'aténuation due au fait que l'énergie sonore émise par une source se répartit sur tout son front d'onde. Or plus le récepteur est loin de la source, plus le front d'onde est étendu, et plus la part de l'énergie sonore reçue par le récepteur devient petite.
. . D'autre part, sur 13 km, le signal sonore émis subira un amortissement du fait des obstacles rencontrés ...
Enfin, pour que le son de la cloche soit discernable, il faudrait que dans un rayon de 13 km autour du récepteur, aucun autre son ne se fasse entendre et ne vienne perturber l'expérience.
D'après l'énoncé de l'exercice, la propagation du son dans l'eau se fait à la fois plus rapidement (9,4 s au lieu de 39,7 s) et avec un moindre amortissement (puisque le son est audible à 13 km).
Remarque : Une des raisons pour laquelle le son est audible dans l'eau est que le fond du lac ainsi que la surface de l'eau réflechissent et canalisent les sons (alors que dans l'air une énorme partie de l'énergie sonore émise est perdue).
c) Calcul de la célérité du son dans l'eau :
v =
. . A.N. . . v = = 1,43 . 103 m.s-1.
Actuellement on considère que la célérité du son dans l'eau est plutôt de 1,5 . 103 m.s-1, mais il faut saluer l'exploi d'une mesure aussi précise il y a près de 180 ans !
d) Il y a 2 siècles, la précision des mesures de temps de l'ordre de la seconde ou du dixième de seconde, nécessitait de faire une expérience durant plusieurs secondes, donc sur une distance de plusieurs kilomètres.
Actuellement, avec un oscilloscope, on peut facilement mesurer des durées de l'ordre de 10 ou 100 microsecondes. Il suffit donc d'une colonne d'eau de quelques décimètres pour faire les mesures. Ce qui permet de faire des mesures de célérité à l'intérieur du laboratoire.
Concrètement, il faut un émetteur et un récepteur d'ultrasons qui peuvent être immergés dans l'eau et positionnés l'un en face de l'autre à une distant d, et d'un oscilloscope.
L'émetteur est relié à la voie 1 de l'oscilloscope et génère des salves d'ultrasons; alors que le récepteur relié à la voie 2 reçoit ces salves avec un retard t dépendant de son éloignement.
Après la mesure précise de d et t, il suffit de calculer v (v = d/t).

