Exercice 1B
Enoncé :
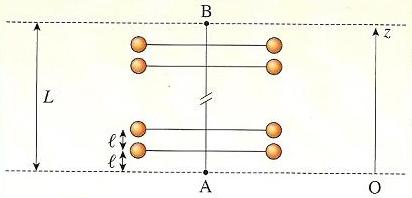
Une échelle de perroquet comporte 41 barreaux régulièrement répartis comme l'indique le schéma.
La longueur du ruban d'acier est L = 2,10 m.
A l'instant t = 0, le premier barreau est écarté, puis ramené dans sa position d'équilibre.
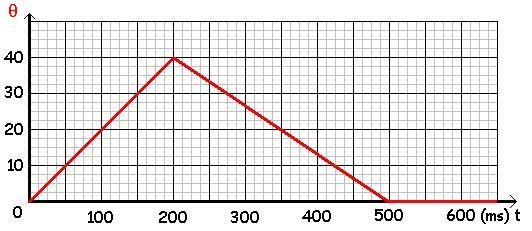
Dans le tableau suivant, on donne son élongation angulaire à différentes dates t.
L'élongation angulaire est nulle pour t < 0 ms et pour t > 500 ms.
a) Quelle est l'amplitude du signal ?
b) Le front d'onde met 4,0 s pour atteindre le barreau 41. En déduire la valeur de la célérité v.
c) Calculer la valeur de la position du front d'onde à la date t = 600 ms.
d) Exprimer le retard du mouvement d'un barreau quelconque, en fonction de son abscisse z et de la célérité v.
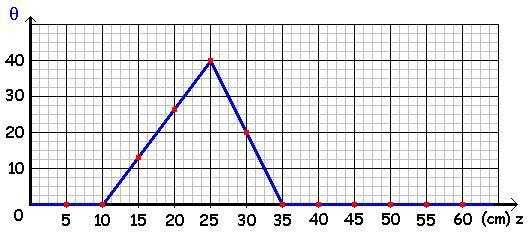
e) Représenter l'élongation θ en fonction de l'abscisse z du barreau à la date t = 600 ms.
f) Après réflexion sur l'extrémité de l'échelle, on observe un signal réfléchi, d'élongation θ négative et d'amplitude 20°. Pourquoi l'élongation θ est-elle négative ?
Quelle est la fraction d'énergie mécanique perdue pendant la réflexion, sachant que l'énergie mécanique transportée est proportionnelle au carré de l'amplitude ?
Solution :
a. L'amplitude étant l'élongation maximale de la déformation, elle est ici égale à 40°.
b. Le front d'onde met 4 s pour aller du 1er au 41ème barreau, ce qui correspond à la distance : D = L - 2 l.
Calculons la valeur de l, sachant que l = `L/(42)`
. . . . A.N. : . . . . . . . l = `(2,10)/(42)` = 0,050 m.
La célérité de l'onde est donc : v = `D/t`
. . . . A.N. : . . . . . . . v = `(2,00)/(4,0)` = 0,50 m.s-1.
c. Calculons le déplacement d du front d'onde pendant la durée t = 600 ms, sachant que d = v . t.
. . . . A.N. : d = 0,50 x 0,600 = 0,30 m.
La distance d correspond exactement à un déplacement de 6 barreaux.
Sachant qu'à t = 0, le front d'onde est au 1er barreau, il sera au 7ème barreau, à t = 0,600 s.
d. A t = 0, le front d'onde est à z1 = l.
A l'instant t (quelconque), le front d'onde sera à l'abscisse z telle que : (z - z1) = v . t
. . . . D'où : . . . . . . . . . . . . . . (z - l) = v . t
Le retard du front d'onde pour arriver à l'abscisse z est donc : t = `(z-l)/v` .
e. Représentons l'élongation θ du 1er barreau en fonction du temps :
A t = 600 ms, le front d'onde s'étant déplacé de 30 cm est au point d'abscisse 35 cm (d'après c.)
En remarquant qu'en 100 ms, le front d'onde se déplace de la distance l séparant 2 barreaux successifs, on obtient le graphe θ = f(z) où les barreaux sont représentés par un carré rouge :
f. L'élongation θ est négative après la réflexion parce que l'extrémité de l'échelle de perroquet est fixe.
L'énergie mécanique E transportée par l'onde étant proportionnelle au carré de l'amplitude A de la déformation, on a :
E = k . A2
D'où, à l'aller : E1 = k . A12
. . . . A.N. : E1 = k x 402 = 1600 k
et au retour : E2 = k . A22
. . . . A.N. : E2 = k x 202 = 400 k
L'énergie perdue lors de la réflexion est : E1 - E2.
La fraction d'énergie perdue pendant la réflexion est : f = `(E_1 - E_2)/(E_1)`
. . . . A.N. : f = `(1600 k - 400 k)/(1600 k)` = `(1200)/(1600)` = 0,75
C'est-à-dire que 75% de l'énergie mécanique est perdue lors de la réflexion.