Exercice 3B

 

Exercice sans calculatrice

 

Enoncé

 

On traite 2,0 g de carbonate de calcium CaCO₃ par 100 mL d’une solution d’acide à 0,100 mol.L^-1.

On observe la réaction :

CaCO_{3 (s)} + 2 H₃O⁺_(aq) = Ca²⁺_(aq) + CO_{2 (g)} + 3 H₂O

a) Calculer les quantités de matière initiales.

Donnée : . .Masse molaire de CaCO3 = 100 g.mol^-1.

b) Faire un tableau d’avancement de la réaction.

c) Calculer la concentration finale des ions calcium.

d) Proposer une méthode physique permettant de suivre la réaction.

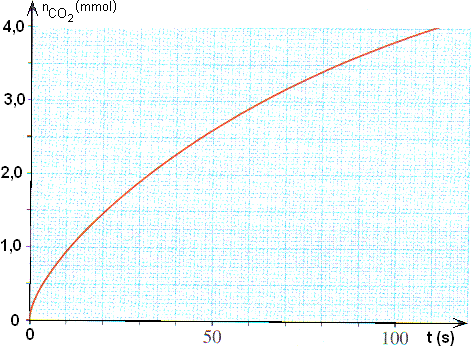
e) On obtient la courbe de la fig.1.

 

 

Définir puis déterminer le temps de demi-réaction t_1/2.

 

 

 

 

 

 

 

 

 

 

Solution

 

a) Calcul des quantités de matière initiales :

Soient n₁ et n₂ (respectivement) les quantités de matière initiales de carbonate de calcium et d'ions oxonium.

. . . . . .n₁ = `m<sub>1</sub>/M<sub>1</sub>`

. . . . . .A.N. : . . n₁ = `(2,0)/(100)` = 2,0 . 10^-2 mol.

. . . . . .n₂ = c₂ . V₂

. . . . . .A.N. : . . n₂ = 0,100 . 0,100 = 1,00 . 10^-2 mol.

 

b) Tableau d'avancement :

 

Etat	Avancement	CaCO3 (s)	+ 2 H3O+(aq) =	Ca2+(aq)	+ CO2 (g)	+ 3 H2O(l)
E.I.	0	2,0 . 10-2	1,00 . 10-2	0	0	solvant
en cours	x	2,0 . 10-2 - x	1,00 . 10-2 - 2x	x	x	solvant
E.F.	xmax=5,0.10-3 mol	1,5 . 10-2	0	5,0.10-3	5,0.10-3	solvant

 

Calcul de l'avancement maximal :

. . . . . .Pour le carbonate de calcium : . . x_max = 2,0 . 10^-2 mol ;

. . . . . .Pour les ions oxonium : . . x_max = 5,0 . 10^-3 mol.

D'où : . . . . . .L'avancement maximal est : x_max = 5,0 . 10^-3 mol

 

c) La quantité de matière finale des ions calcium est n(Ca²⁺) = n_f = x_max = 5,0 . 10^-3 mol.

D'où la concentration : . . [Ca²⁺] = `n_f/V` . .où V est le volume du milieu réactionnel ;

. . . . . .A.N. : . . [Ca²⁺] = `(5,0.10^-3)/(0,100)` = 5,0 . 10^-2 mol.L^-1.

 

d) L'avancement étant égal à la quantité de gaz (CO₂) formé, pour suivre l'avancement de la réaction, il suffit de mesurer la pression du gaz formé au cours du temps.

 

e) Par définition, le temps de demi-réaction est le temps nécessaire pour que l'avancement évolue de 0 à x_max/2; soit ici 2,5 . 10^-3 mol.

D'après la courbe de la fig.1, le temps correspondant à l'avancement 2,5 . 10^-3 mol est t_1/2 = 47 s.