D.S.2 du 09/11/10

 

Chimie :

 

1. Absorbance de différentes solutions de caféine.

1.a. Pour utiliser le spectrophotomètre, il faut :

. . . . . . . 1) choisir la longueur d'onde λ = 271 nm;

. . . . . . . 2) faire le zéro avec une cuve contenant de l'eau distillée.

 

1.b. La droite d'étalonnage est obtenue en mesurant l'absorbance de différentes solutions de caféine de concentrations connues.

 

1.c. Sachant que l'absorbance A est proportionnelle à la concentration c en caféine, on a : . . A = k . c

Le coefficient de proportionnalité k peut être obtenu en écrivant : . . k = `A/c`

. . . . . . . A.N. : . . k = `(0,30)/(0,010)` = 30 L.g^-1.

 

1.d. Calculons la concentration dont l'absorbance est égale à 0,54 , sachant que : . . A = k . c

. . D'où :

c = `A/k`

. . . . . . . A.N. : . . c = `(0,54)/(30)` = 0,018 g.L^-1 = 18 mg.L^-1.

 

1.e. Sur le document 1, on voit que la solution utilisée a une absorbance égale à 0,50 pour λ = 271 nm;

et sur le document 2, on voit que pour λ = 271 nm, l'absorbance égale à 0,50 est obtenue avec une concentration en caféine de 17 mg.L^-1. La solution utilisée a donc une concentration en caféine de 17 mg.L^-1.

 

 

Physique :

 

2. Diffraction d'un faisceau laser.

2.a. Le faisceau laser de longueur d'onde λ = 650 nm a une couleur rouge (limite orange/rouge).

 

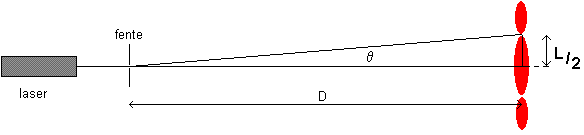
2.b. On obtient une figure de diffraction composée de taches de largeur d autour d'une tache centrale de largeur L = 2 d.

 

 

2.c. Soit θ l'angle sous lequel la demi-tache centrale est vue depuis la fente :

 

 

2.d. D'après la figure de la question précédente, on a :

tan θ = `(L/2)/D` = `L/(2 D)`

 

2.e. Si l'angle θ est petit, alors : θ = tan θ , d'où :

θ = `L/(2 D)`

 

2.f. Pour une figure de diffraction provoquée par une fente de largeur a, la demi-largeur angulaire de la tache centrale est telle que :

θ = `(λ)/a`

 

2.g. On obtient donc la relation :

θ = `(λ)/a` = `L/(2 D)`

. . . . . . . D'où :

a = `(D * 2 * λ)/L`

. . . . . . . A.N. : . . . a = `(3 * 2 * 650 * 10^-9)/(13 * 10^-2)` = `(3 * 1300 * 10^-9)/(13 * 10^-2)` = 3,0 . 10^-5 = 30 µm.

 

2.h. Avec un laser de lumière verte (λ' = 520 nm environ), l'angle θ obtenu avec la même fente de largeur a serait plus petit (puisque la longueur d'onde est plus petite), donc toute la figure de diffraction serait plus resserrée.

 

 

3. Désintégration radioactive d'un noyau de bismuth 210.

3.a. La désintégration α s'écrit :

`{::}_83^210`Bi —> `{::}_81^206`Tl + `{::}_2^4`He

 

3.b. La désintégration β^- s'écrit :

`{::}_83^210`Bi —> `{::}_84^210`Po + `{::}_(-1)^0`β^-

 

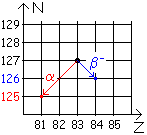
3.c. Représentons ces 2 désintégrations dans le diagramme N-Z :

 

 

 

4. Activité d'un échantillon de noyaux radioactifs.

4.a. La demi-vie t_½ d’un isotope radioactif est la durée au bout de laquelle la moitié des noyaux radioactifs de l'échantillon se sont désintégrés.

D'après la définition de la demi-vie t_½, on a :

N(t_½) = `N_0` . e^-`λ`.t½ = `(N_0)/2`

. . . . D'où :

e^-`λ`.t½ = `1/2`

. . . . D'où :

e^`λ`.t½ = 2

. . . . D'où :

`λ` . t_½ = ln 2

 

4.b. La quantité de matière n₀ (nombre moles) de noyaux radioactifs présents initialement dans l'échantillon est :

n₀ = `(m_0)/M`

Le nombre N₀ de noyaux radioactifs présents initialement dans l'échantillon est donc :

N₀ = n₀ . N_A = `(m_0)/M` . N_A

 

4.c. L'activité de l'échantillon est :. . A(t) = λ . N(t)

. . . . .D'où : . . . . . A₀ = λ . N₀

Unités : pour avoir l'activité en becquerel, il faut exprimer la constante radioactive en s^-1, N étant un nombre de noyaux.

 

4.d. Le tableau suivant donne la proportion de noyaux radioactifs restant :

 

instant t	proportion	masse des noyaux
t0 = 0	100 %	8,0 mg
t1 = t½ = 30 min	50 %	4,0 mg
t2 = 2 x t½ = 60 min	25 %	2,0 mg
t3 = 3 x t½ = 90 min	12,5 %	1,0 mg
t4 = 4 x t½ = 2 heures	6,3 %	0,50 mg

 

4.e. Les grandeurs caractéristiques d’un type de noyaux radioactifs sont : la demi-vie t_½ ; la constante radioactive λ et la constante de temps τ.