
Chap.2 Ondes mécaniques progressives périodiques
Introduction
Dans le chapitre précédent, nous avons étudié la propagation d'une perturbation dans un milieu matériel élastique. Nous avons vu que si une déformation apparaît en un point, elle pourra se propager sous forme d'une onde mécanique progressive dans tout le milieu. Mais une fois que l'onde est passée, chaque point déplacé revient à sa position initiale.
Dans ce nouveau chapitre, nous allons étudier le cas particulier des milieux qui sont soumis (pendant un temps plus ou moins long) à une déformation périodique (c'est-à-dire une déformation de même forme, survenant à intervalle de temps régulier).
1. Définitions
On appelle source S, le point du milieu où la déformation est créée.
La source S a un mouvement périodique si son mouvement se reproduit (identiquement) à intervalle de temps régulier.
Une onde mécanique progressive est périodique si l’onde se propageant dans le milieu considéré, se reproduit (identiquement) à intervalle de temps régulier.
. . . . . Exemples :
. . . . . . . . - la vibration périodique d'une pointe en contact avec la surface de l'eau, génère des ondes circulaires périodiques ;
. . . . . . . . - la vibration périodique d'un électro-aimant relié à une corde élastique peut donner naissance à des ondes périodiques ;
. . . . . . . . - la vibration périodique d'une corde de violon, d'une anche d'une clarinette ou des cordes vocales provoque l'apparition d'un son régulier ;
. . . . . . . . - les vagues ou la houle à la surface des mers peuvent également être considérées comme un phénomène quasiment périodique.
La période T est la durée au bout de laquelle le phénomène se reproduit.
. . . . . L'unité de mesure de la période est la seconde (s).
. . . . . Remarque : La période de l'onde est la même que celle de la source qui lui a donné naissance.
La fréquence `ν` est égale au nombre de périodes par seconde.
. . . . . L'unité de mesure de la fréquence est le hertz (Hz).
. . . . . La relation entre la fréquence et la période est : . . . . . `ν = 1/T`
2. Double périodicité
2.a. Périodicité temporelle
Etant donné, d'une part, que la source S a un mouvement périodique, et d'autre part, que tout point M du milieu considéré reçoit la déformation initialement en S avec un retard dépendant de la distance entre ces 2 points, le mouvement du point M sera périodique de même période T que la source.
On peut donc dire que tout point recevant la déformation est animé d'un mouvement périodique semblable à celui de la source.
On peut représenter la déformation de la source par une fonction périodique u(t), où u est l'élongation qui sera mesurée en mètre, en degré, en pascal, etc ... suivant qu'il s'agit d'un déplacement, d'une torsion, d'une pression, etc ...
Considérons une source soumise à la déformation suivante :
ligne
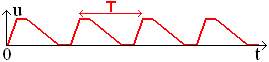
ligne
T est la période temporelle du mouvement. Elle s'exprime en seconde.
2.b. Périodicité spatiale
Etant donné, d'une part, que la source S a un mouvement périodique, et d'autre part, que tout point M du milieu considéré reçoit la déformation initilament en S avec un retard dépendant de la distance entre ces 2 points, à tout instant, la déformation du milieu sera périodique dans l'espace.
On peut donc dire qu'à tout instant, les différents points recevant la déformation sont régulièrement répartis dans le milieu considéré.
Pour l'onde créée par la source étudiée précédemment, on peut représenter la déformation du milieu à un instant t donné, par une fonction périodique u(x) suivante :
ligne
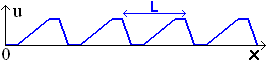
ligne
L est la période spatiale de l'onde. Elle s'exprime en mètre.
2.c. Remarques :
. . Les 2 graphes u(t) et u(x) se ressemblent mais sont "inversés" l'un par rapport à l'autre. En effet, le début de la déformation de la source (à gauche sur le graphe u(t)) a eu plus de temps que la suite de la déformation pour se propager. Il est donc arrivé plus loin dans l'espace (à droite sur le graphe u(x)).
. . Si, lors d'une expérience faite en laboratoire, on voulait créer 2 documents expérimentaux permettant de visualiser, l'un u(t) et l'autre u(x), comment s'y prendrait-on ?
. . . . . Pour visualiser u(t) on filmerait le mouvement d'un point (par exemple la source) au cours du temps.
. . . . . Pour visualiser u(x) on photographierait l'ensemble de l'espace à un instant donné.
. . . . . Le graphe u(t) représente la déformation en un point donné au cours du temps (x fixe et t variable).
. . . . . Le graphe u(x) représente la déformation à un instant donné le long de l'espace (t fixe et x variable).
. . Si la célérité de l'onde dans le milieu considéré est c, les périodes spatiale et temporelle sont reliées par la relation :
L = c . T
2.d. Cas particulier d'une onde sinusoïdale
. . Lorsque l'onde a une forme sinusoïdale, la période spatiale est appelée "la longueur d'onde".
ligne

ligne
. . La longueur d'onde, notée `λ`, est donc la distance parcourue par l'onde pendant une période.
. . . . . D'où la relation :
`λ` = c . T
. . . . . ou bien : . . . . . `λ = c/ν`
. . . . . L'unité de mesure de la longueur d'onde est le mètre (m).
Propriétés remarquables :
Dans un milieu à 1 dimension, 2 points M1 et M2 vibrent en phase si leur distance est égale à un nombre entier k de longueur d’onde.
Sur la figure suivante, la distance entre M1 et M2 (notée [M1M2]) est égale à 2 longueurs d’onde (k = 2).
ligne
ligne

ligne
. . . . . D'où la relation :
[M1M2] = k . `λ`
La distance entre M1 et M2 étant égale à k . `λ`, le point M2 reçoit l’onde avec un retard τ par rapport à M1, tel que :
τ = k . T
Dans un milieu à 1 dimension, 2 points M1 et M2 vibrent en opposition de phase si leur distance est égale à un nombre impair (2k+1) de demi-longueur d’onde.
Sur la figure suivante, la distance entre M1 et M2 est égale à 1 longueur d’onde + une demi-longueur d’onde (k = 1).
ligne
ligne

ligne
. . . . . D'où la relation :
[M1M2] = (2k+1) . `(λ)/2`
La distance entre M1 et M2 étant égale à (2k+1) . `(λ)/2`, le point M2 reçoit l’onde avec un retard τ par rapport à M1, tel que :
τ = (2k+1) . `T/2` .
. . . . . Remarques :
. . . . . Les mêmes relations, pour les points vibrant en phase ou en opposition de phase, peuvent être appliquées dans un milieu à 2 ou 3 dimensions, à condition que les points M1 et M2 soient situés sur une droite parallèle à la direction de propagation.
. . . . . Au contraire, les points situés sur un même front d'onde (localement perpendiculaire à la direction de propagation) vibrent en phase quelque soit leur distance.
3. La dispersion
L'étude de certaines ondes périodiques (comme les ondes à la surface de l'eau) fait apparaître que la célérité peut varier avec la fréquence des ondes.
On dit alors que le milieu est dispersif.
. . . . . Exemple : la célérité des ondes à la surface de l'eau augmente avec la fréquence.
. . . . . On a par exemple :
. . . . . . . . . . . . c = 0,23 m.s-1 pour `ν` = 24 Hz ;
. . . . . . . . . . . . c' = 0,28 m.s-1 pour `ν`' = 48 Hz.
Remarque : L'air n'est pas un milieu dispersif pour les ondes sonores.
Ainsi, lorsqu'on assiste à un concert, la musique jouée par la basse (`ν` < 100 Hz) et le chant aigu de la soliste (`ν` > 1000 Hz) sont toujours parfaitement synchronisés, quelque soit notre distance de la scène. La célérité de ces 2 sons est donc bien la même.
4. La diffraction
L'expérience montre que les ondes semblent se comporter différemment lorsqu'elles passent à travers une ouverture large ou étroite.
Observons le cas des ondes à la surface de l'eau.
| Caractéristiques : |
|
|
| Ondes rectilignes |
|
|
| obstacle rectiligne |
|
|
| fente large |
|
|
| fente étroite |
|
|
Commentaire : La source des vibrations étant rectiligne, les ondes crées à la surface de l'eau sont rectilignes.
S'il n'y avait pas de phénomène de diffraction, on s'attendrait à ce que, à l'abord d'un obstacle, la partie des ondes qui peut continuer à se propager en ligne droite poursuive sa trajectoire, alors que celle qui rencontre l'obstacle soit arrêtée.
Cela correspond assez bien à ce qui est observé avec l'obstacle rectiligne ou avec la fente large.
Par contre, quand la fente est étroite, il apparaît un phénomène nouveau : l'ouverture se comporte comme une source d'onde circulaires !
On dit que les ondes sont diffractées lors du passage par cette ouverture étroite.
La diffraction est le changement de direction d’une onde au passage d’une petite ouverture ou à proximité d’un obstacle.
L'importance de ce phénomène dépend de la taille relative de l'obstacle par rapport à la longueur d'onde.
La diffraction se manifeste lorsque la largeur de l’ouverture ou de l’obstacle est de l'ordre de quelques longueurs d'onde.
. . . . . On peut dire, par exemple, que le phénomène de diffraction apparaît avec les ondes mécaniques lorsque la largeur de l'ouverture est inférieure à 5 `λ`.
De plus, le phénomène de diffraction augmente lorsque la largeur de l'ouverture diminue.
Bien qu'il soit difficile à visualiser, le phénomène de diffraction a une importance pratique pour les sons.
En voici quelques conséquences :
. . . . . - les sons semblent contourner les obstacles ;
. . . . . - en plein air, on peut entendre des sons provenant d'une source cachée par un obstacle de taille limitée ;
. . . . . - les sons graves (basse fréquence, donc grande longueur d'onde) se propagent mieux dans un bâtiment que les sons aigus (haute fréquence, donc petite longueur d'onde) en étant davantage diffractés par les portes ouvertes.








