Exercice n° 21 p. 50

 

a. Vu de la Terre, le satellite Io disparaît chaque fois que dans son mouvement de rotation il passe derrière Jupiter.

 

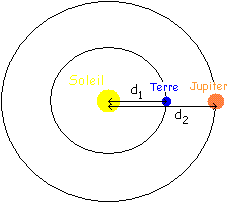
b. La distance à parcourir par la lumière dépend des positions respectives de la Terre et de Jupiter par rapport au Soleil.

 

. . . . .

 

c. D'après les schémas précédents, la différence entre les distances parcourues par la lumière entre Jupiter et la Terre est égale au diamètre de l'orbite de le Terre autour du Soleil.

 

d. Sachant que l'écart de 16 minutes correspond au temps mis par la lumière pour parcourir la distance 2 d₁, on peut écrire :

2 d₁ = v . t

D'où :

d₁ = ½ . v . t

A.N. : d₁ = ½ . 2,12 . 10⁵ . 16 . 60 = 102 . 10⁶ km.

 

Remarque : En réalité, la distance d₁ (rayon de l'orbite de la Terre autour du Solel) est égale à 150 . 10⁶ km.

La méthode de calcul proposée par Römer est juste, mais la valeur de d₁ connue à l'époque étant fausse, la valeur numérique du résultat est faux (mais son ordre de grandeur est juste ce qui est un grand progrès!).

 

Sur le site du Club Astronomique du Val de Loir, il y a une intéressante page relatant l'histoire de la mesure de la vitesse de la lumière.