Exercice 5C
Enoncé :
Un pendule est constitué d'une bille de centre C et de masse m = 100 g reliée à un point fixe O par un fil inextensible de longueur l = 50 cm et de masse négligeable.
On écarte le pendule de sa position d'équilibre d'un angle θ0 = 30° et on le lâche sans vitesse initiale.
On note θ l'angle entre le fil et la verticale à un instant quelconque.
;
a. Calculer le travail du poids de la bille lorsque θ passe de θ0 à 0.
b. Donne l'expression du travail du poids de la bille lorsque l'angle varie de θ0 à θ.
c. Calculer le travail du poids de la bille lorsque θ passe de θ0 à -θ0.
d. Peut-on écrire que le travail de la tension `vec{T}` du fil entre 2 points A et B est égale à `vec{T}` . `vec{AB}` ? Justifier.
e. Quel est la valeur du travail de la tension du fil dans les 2 cas étudiés précédemment ?
Solution :
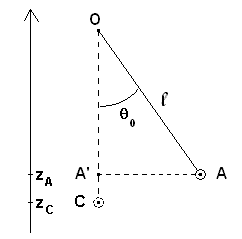
a. Soit C la position de la bille à la verticale du point O.
Calculons le travail du poids lorsque θ passe de θ0 à 0, c'est-à-dire lorsque la bille passe de A en C.
. . . . . . . WAC (`vec{P}`) = `vec{P}` . `vec{AC}` = P . AC . cos(`vec{P}`,`vec{AC}`) = m . g . (zA - zC)
. . . . . . . Or : . . zA - zC = A'C
On peut remarquer que A'C = OC - OA'
. . . . . . . Or : . . OC = l . . et . . OA' = l . cos θ0.
. . . . . . . D'où : . . zA - zC = l - l . cos θ0 = l (1 - cos θ0).
. . . . . . . D'où : . . WAC (`vec{P}`) = m . g . l (1 - cos θ0).
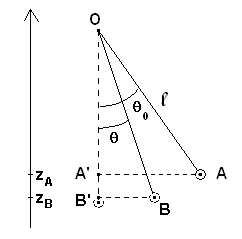
b. Cherchons l'expression du travail du poids lorsque l'abscisse angulaire varie de θ0 à θ, c'est-à-dire lorsque la bille va de A en B.
. . . . . . . WAB (`vec{P}`) = `vec{P}` . `vec{AB}` = P . AB . cos(`vec{P}`,`vec{AB}`) = m . g . (zA - zB)
. . . . . . . Or : . . zA - zB = A'B' = OB' - OA'
. . . . . . . D'où : . . zA - zB = OB' - OA' = l . cos θ - l . cos θ0 = l . ( cos θ - cos θ0)
. . . . . . . D'où : . . WAB (`vec{P}`) = m . g . l (cos θ - cos θ0).
c. Calculons la valeur du travail du poids lorsque l'abscisse angulaire varie de θ0 à -θ0:
D'après la relation précédente, on a : . . WAB (`vec{P}`) = m . g . l (cos (-θ0) - cos θ0)
. . . . . . . or : . . cos (-θ0) = cos θ0.
. . . . . . . D'où : . . WAB (`vec{P}`) = m . g . l (cos (-θ0) - cos θ0) = 0
d. Dans le cours, on a défini le travail d'une force constante : . . WAB (`vec{F}`) = `vec{F}` . `vec{AB}`
Or, la tension `vec{T}` n'est pas constante car sa direction varie en fonction de l'abscisse angulaire θ, on ne peut donc pas utiliser la relation du cours pour un déplacement `vec{AB}` trop grand.
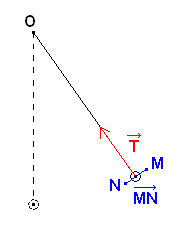
e. Mais on peut calculer ce travail de la tension `vec{T}`, en remarquant que pour un déplacement `vec{MN}` suffisamment petit pour que la tension `vec{T}` puisse être considérée comme constante, on a `vec{T}` perpendiculaire à `vec{MN}`.
En effet, la tension `vec{T}` est un vecteur dirigé vers O, le centre du cercle, alors que le vecteur déplacement `vec{MN}` a une direction tangente au cercle.
Donc, à tout instant : . . WMN (`vec{T}`) = `vec{T}` . `vec{MN}` = T . MN . cos 90 = 0
Si le travail de la tension est nul, quelque soit la position de la bille, pour un petit déplacement sur le cercle, on peut dire que le travail de la tension est toujours nul (car à tout instant la tension est perpendiculaire au déplacement).
On peut donc en conclure que WAC (`vec{T}`) = 0
. . . . . . . De même : . . WAB (`vec{T}`) = 0.