D.S.2 du 12/11/10

 

Chimie :

 

1.a. Tableau d’avancement de la réaction :

 

Etat	Avancement	Zn	+ 2 H+	`to` Zn2+	+ H2
E.I.	0	0,100	0,150	0	0
en cours	x	0,100 - x	0,150 - 2 x	x	x
E.F.	xmax	0,100 - xmax	0,150 - 2 xmax	xmax	xmax

 

1.b. Calcul de l’avancement maximal :

. . . . . . - pour le zinc Zn :. .x_max = 0,100 mol ;

. . . . . . - pour les ions H⁺ :. .x_max = 0,150 / 2 = 0,075 mol.

donc les ions hydrogène sont le réactif limitant et x_max = 0,075 mol.

 

1.c. Le réactif en excès est le métal zinc.

 

1.d. La concentration molaire des ions H⁺ est c = `n/V`

. . . . . . A.N. :. .c = `(0,150)/(0,100)` = 1,50 mol.L^-1.

 

1.e. La masse initiale de zinc est :. .m = n . M

. . . . . . A.N. :. .m = 0,100 . 65,4 = 6,54 g.

 

1.f. Le volume du gaz H₂ peut être obtenu à partir de 2 relations :

. . . . . . - la relation du gaz parfait :. .P . V = n . R T

. . . . . . . . . . . . . . avec P en Pa,. .V en m³,. .n en mol. .et. .T en K ;

. . . . . . - la relation des gaz :. .V = n .V_m

. . . . . . . . . . . . . . avec V en L,. .n en mol. .et. .V_m en L.mol^-1.

 

 

Physique :

 

2. Forces appliquées à la poutre en équilibre

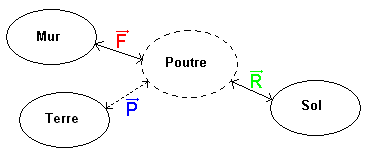
2.a. Diagramme objets/interactions :

 

 

La poutre subit 3 interactions : une interaction à distance avec la Terre et deux interactions de contact (avec le mur et le sol).

La poutre est donc soumise à 3 forces : son poids `vec{P}` et la réaction du mur `vec{F}` et celle du sol `vec{R}`.

 

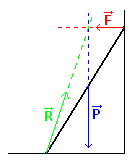
2.b. Schéma des forces appliquées à la poutre.

 

 

2.c. Caractéristiques des forces :

 

Le poids `vec{P}` :

. . . . . . - direction : verticale

. . . . . . - sens : ascendant

. . . . . . - valeur : P = m g.

 

La réaction du mur `vec{F}` :

. . . . . . - direction : horizontale car la réaction est normale (perpendiculaire au mur) puisqu'il n'y a aucun frottement

. . . . . . - sens : du mur vers la poutre

. . . . . . - valeur : F à déterminer.

 

La réaction `vec{R}` :

. . . . . . - direction : selon la droite représentée en vert car les 3 forces sont concourantes

. . . . . . - sens : du sol vers le haut

. . . . . . - valeur : R à déterminer.

 

2.d. La poutre est en équilibre sous l'action de ces 3 forces.

D'après la 1^èreloi de Newton, la poutre tant en équilibre, la somme des forces appliquées est nulle.

. . . . . . D'où :. .`vec{P} + vec{F} + vec{R} = vec{0}`

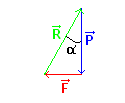
Cette condition peut être représentée par le triangle des forces.

 

 

On obtient :

. . . . . . tan α = `F/P`. . .d'où :. . . F = P . tan α

 

. . . . . . cos α = `P/R`. . .d'où :. . . R = `P/(cos α)`

 

 

3. Rotation de la turbine

3.a. La vitesse angulaire est :. . .ω = 600 tr.min^-1 = 10,0 tr.s^-1.

La fréquence de rotation est donc :. . .f = 10,0 Hz.

La période du mouvement est T telle que : . . . T = `1/f`

. . . . . . A.N. :. .T = `1/(10,0)` = 0,100 s = 100 ms.

3.b. La vitesse angulaire (exprimée en rad.s^-1) est :. . .ω = 2Π .f = 10,0 tr.s^-1.

. . . . . . A.N. :. .ω = 2Π . 10,0 = 62,8 rad.s^-1.

3.c. La vitesse v d'un point situé à la périphérie d'une turbine de rayon R est :. . .v = R . ω

. . . . . . A.N. :. .v = 1,00 . 62,8 = 62,8 m.s^-1.

 

 

4. Forces appliquées au traîneau

4.a. Le temps de marche de l'explorateur est t = 32 jours = 32 x 24 x 3600 s

Sa vitesse moyenne (pendant la marche) est :. .v = `d/t`

. . . . . . A.N. :. .v = `(2845 . 10^3)/(32 x 24 x 3600)`

 

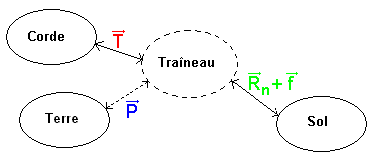
4.b. Diagramme objets/interaction

 

 

L'interaction avec le sol peut être décomposée en 2 forces :

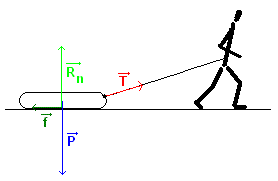
. . . . . . - la réaction normale `vec{R_n}` (qui porte le traîneau) ;

. . . . . . - les frottements `vec{f}` (qui s'opposent au déplacement du traîneau).

 

4.c. D'après la 1^èreloi de Newton, le mouvement du traîneau étant rectiligne uniforme, la somme des forces appliquées est nulle.

. . . . . . D'où :. .`vec{P} + vec{T} + vec{R_n} + vec{f} = vec{0}`

 

4.d. D'où le schéma des forces suivant :